Activity 12.1:
Aim: Calculate the distance between the planets and the Sun in A.U. and ly.
Instruction
Complete the table below.
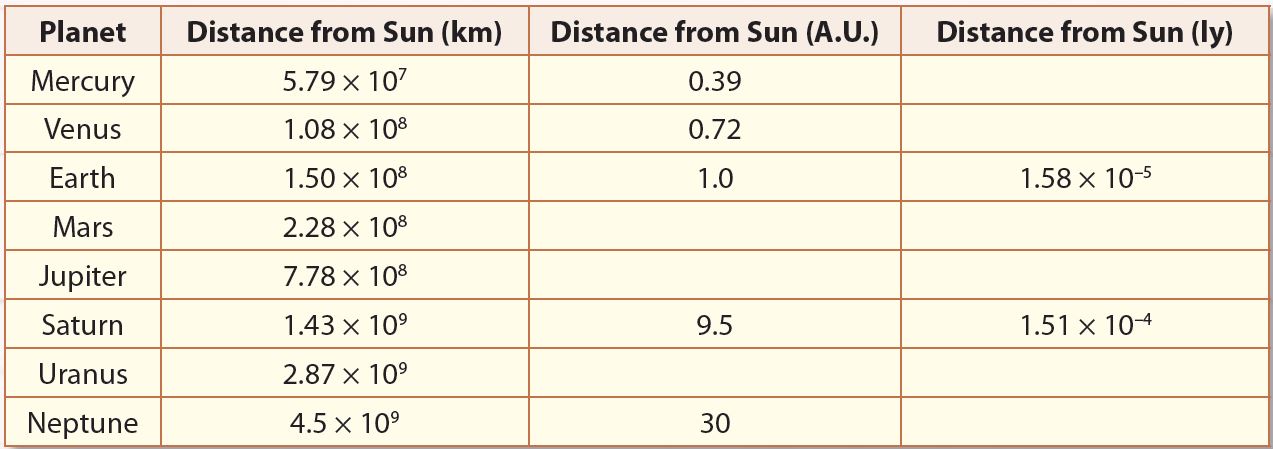
Answer:
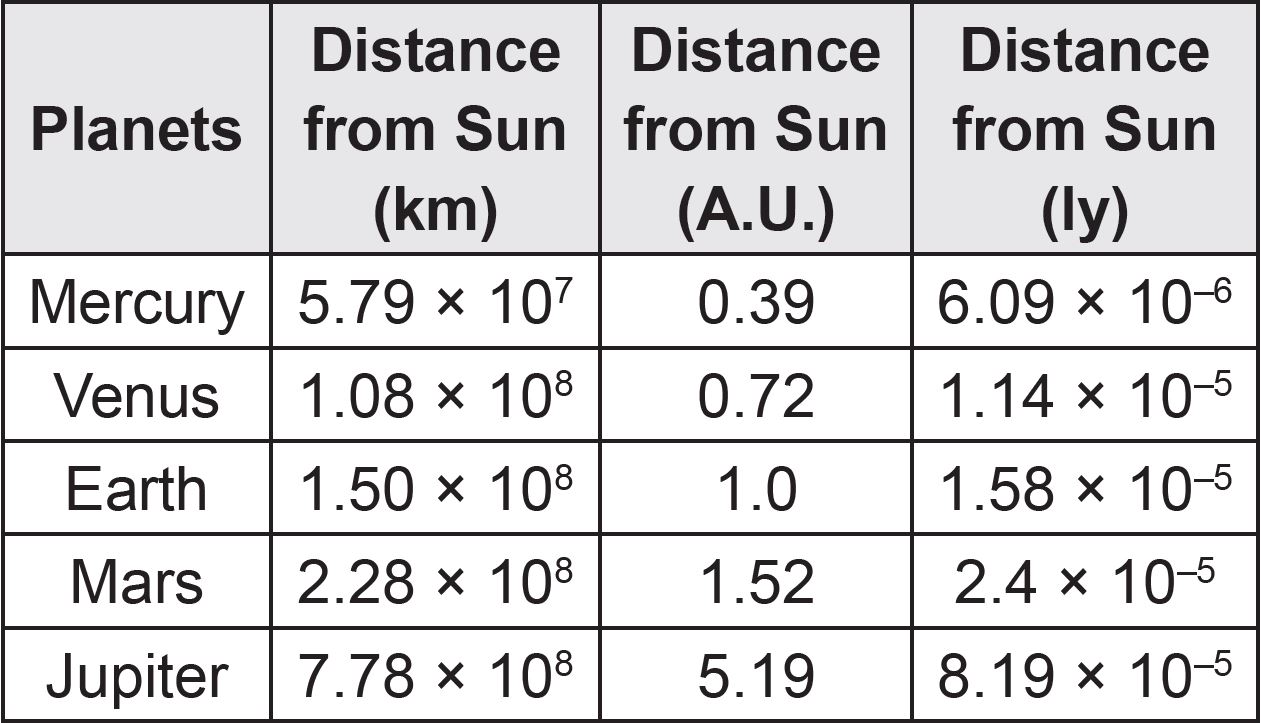
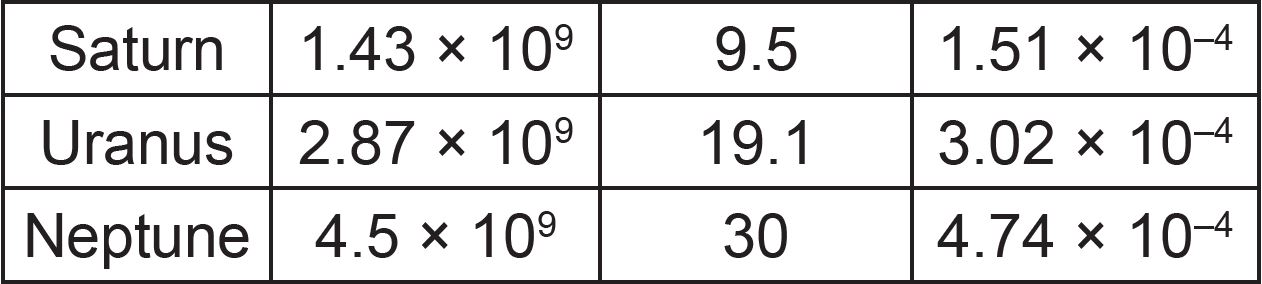
Aim: Calculate the distance between the planets and the Sun in A.U. and ly.
Instruction
Complete the table below.

Answer:

